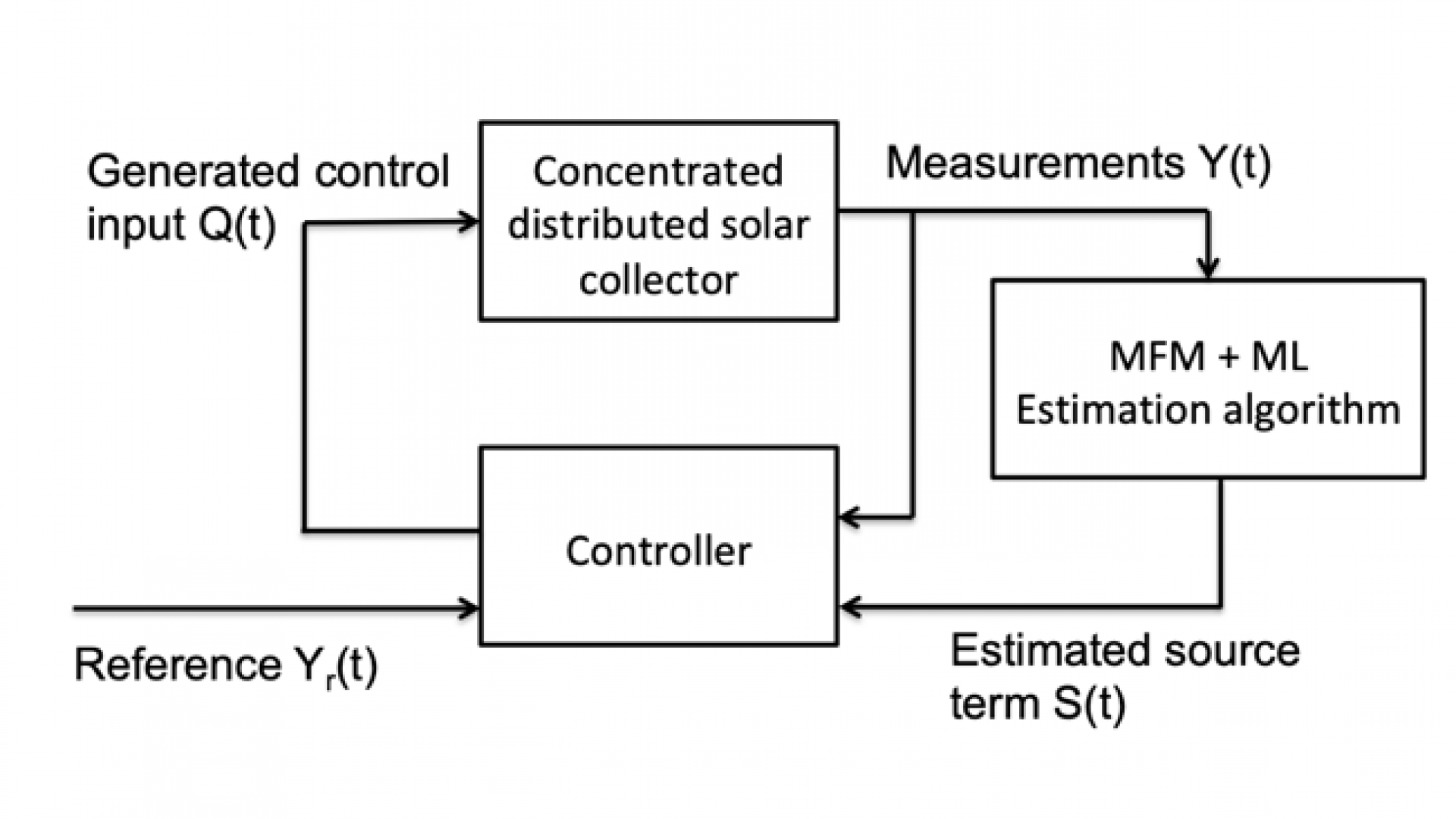
Estimation problems are ubiquitous in control and monitoring of dynamical systems. The most popular approach for the estimation of states is state observers such as the well-known Luenberger observer. Typically, an observer uses a copy of the system model, augmented with an output injection term the gain of which is obtained by ensuring the asymptotic convergence of the state estimation error to zero when time tends to infinity. However, in many situations, convergence of the state in finite time is favorable. Several finite-time convergence estimation algorithms have been proposed for various classes of systems, including linear and nonlinear dynamical systems, distributed parameter systems such as partial differential equations and fractional order systems. Examples of pertinent algorithms are finite-time convergent observers, such as higher order sliding mode observers, algebraic methods and modulating functions approaches.

The following approaches can be considered in the non-asymptotic estimation category:

• Interval observers

• Finite-time convergence in the sense of practical stability

• Prescribed time convergence

• Methods based on direct computation of the solution

• Volterra integral transformation and modulating functions