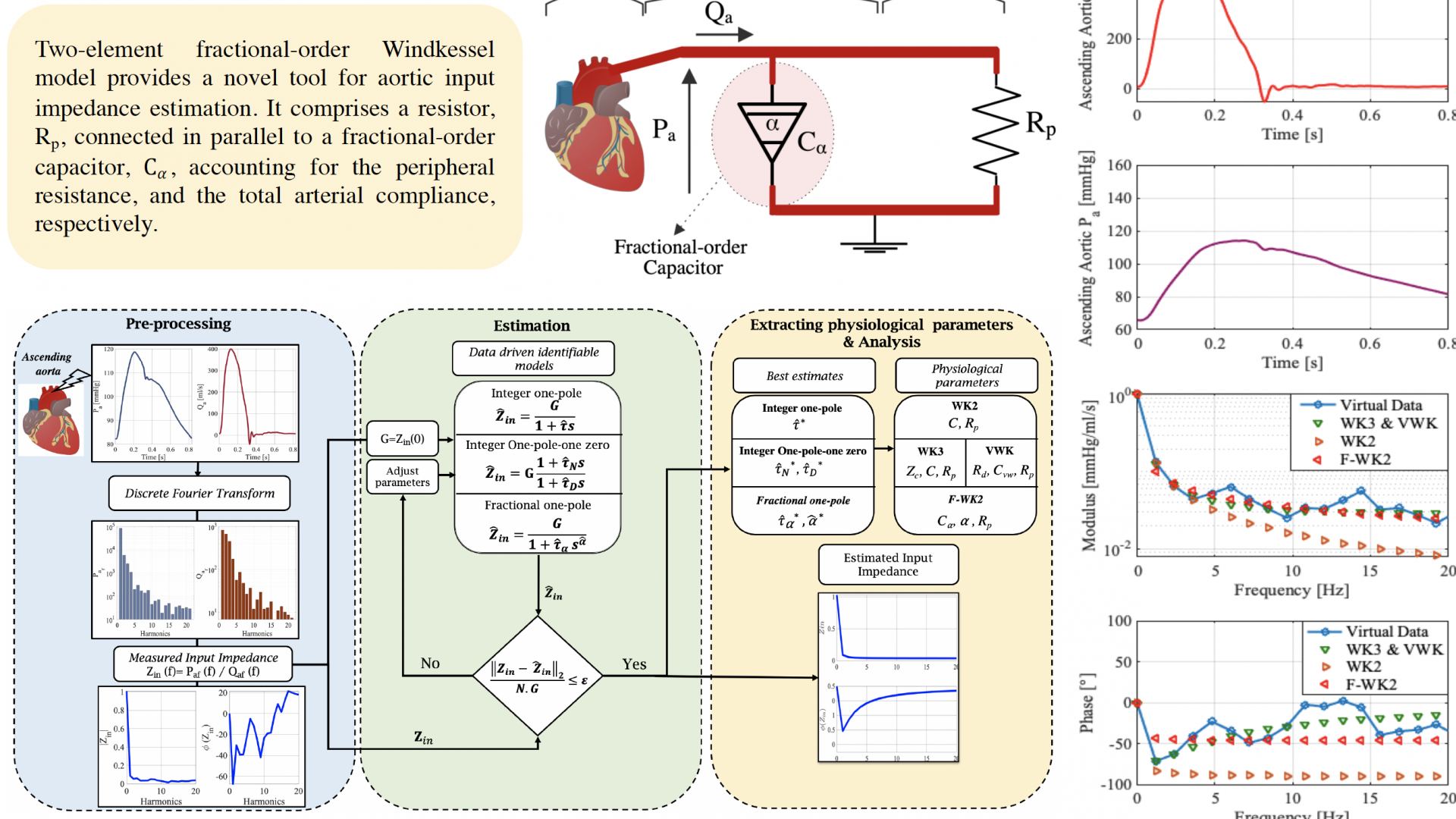
It is commonly recognized that assessing the vascular impedance at the level of the ascending aorta provides valuable information about the physiological state of the cardiovascular system. In this study, Mohamed Bahloul and Prof. Meriem Laleg investigate the arterial Windkessel model within a fractional-order modeling framework. Tools from fractional-order calculus, such as the fractional-order impedance, have been used to estimate the aortic input impedance. The study focused on the FWK2, which includes a fractional-order capacitor. The latter represents both the resistance and compliance properties, reflecting the viscoelastic behavior of the systemic arteries. The contribution of both characteristics can be controlled by the fractional differentiation order, alpha, enabling a reduced-order and flexible representation of the arterial impedance. The validation and comparison with the conventional WK model results show how the proposed model fits better the moduli of the aortic input impedance and fairly approximates the phase angle. Besides, the proposed model’s modulus dynamic compliance at the heart pulsation demonstrated a good correlation with both the static and dynamic compliance of the classical Windkessel models.
In the future, we aim to demonstrate how fractional-order arterial lumped parametric models can easily include the complex effects and the multi-scale features of arterial tissue. This new paradigm deserves consideration as a new framework for solving hemodynamics problems, and in particular, for better understanding of the arterial stiffness dependencies.