Mohamed Ghattassi received his Ph.D. degree in Applied Mathematics and Control Theory from the University Lorraine (IECL-CRAN, Université de Lorraine), France, in 2015. He subsequently spent a year at the University of Lorraine as a research and teaching assistant. Since 2017, he is a Postdoc at the King Abdullah University of Science and Technology (KAUST) in the Computer, Electrical and Mathematical Sciences and Engineering Division (CEMSE). His research interests are in the area of modeling, control and numerical analysis of partial differential equations.
Research Description
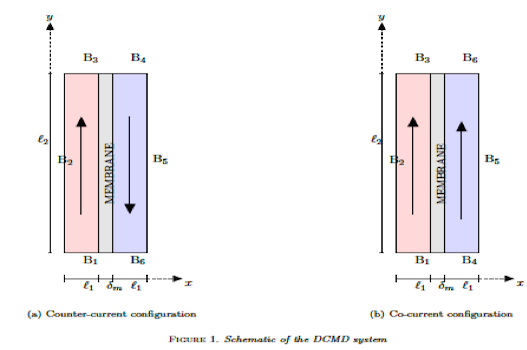
Mohamed Ghattassi is working on control, theoretical and numerical analysis of some class of parabolic-hyperbolic PDEs. He investigated the well-posedness criteria of the coupled radiative-conductive heat transfer in a semi-transparent, gray and non-scattering 2D medium. The model is described by the radiative transfer equation (RTE) and the nonlinear heat equation (NHE). Moreover, He developed a useful algorithm to simulate the temperature in the medium. He used the quadrature SN for the angular discretization of the RTE. The spatial discretization of RTE was made by the Discontinuous Galerkin method (DG) and the finite element method for the nonlinear heat equation. He has shown the convergence and the stability of the coupled numerical scheme. He also proposes a reduced observer design to estimate the temperature for the heat transfer system which ensures the exponential stability of the proposed observer. However, He is interested in the controllability of the heat transfer system. Recently, he investigates the analysis and observers design for the developed mathematical model of a direct contact membrane distillation (DCMD) system. This model consists of a two-dimensional advection-diffusion system coupled at the boundary. Therefore an inverse problem related to the parabolic PDE and (DCMD) system is treated. Finally, He is also interested in the boundary control of the Radiative transfer equation, the controllability of the parabolic system and the diffusion Limits of the parabolic-hyperbolic system in particular for the Heat Transfer System.
Education Profile
- Ph.D. degree in Applied Mathematics and Control Theory from the University Lorraine (IECL-CRAN, Université de Lorraine), France (2015)