© 2018 KAUST
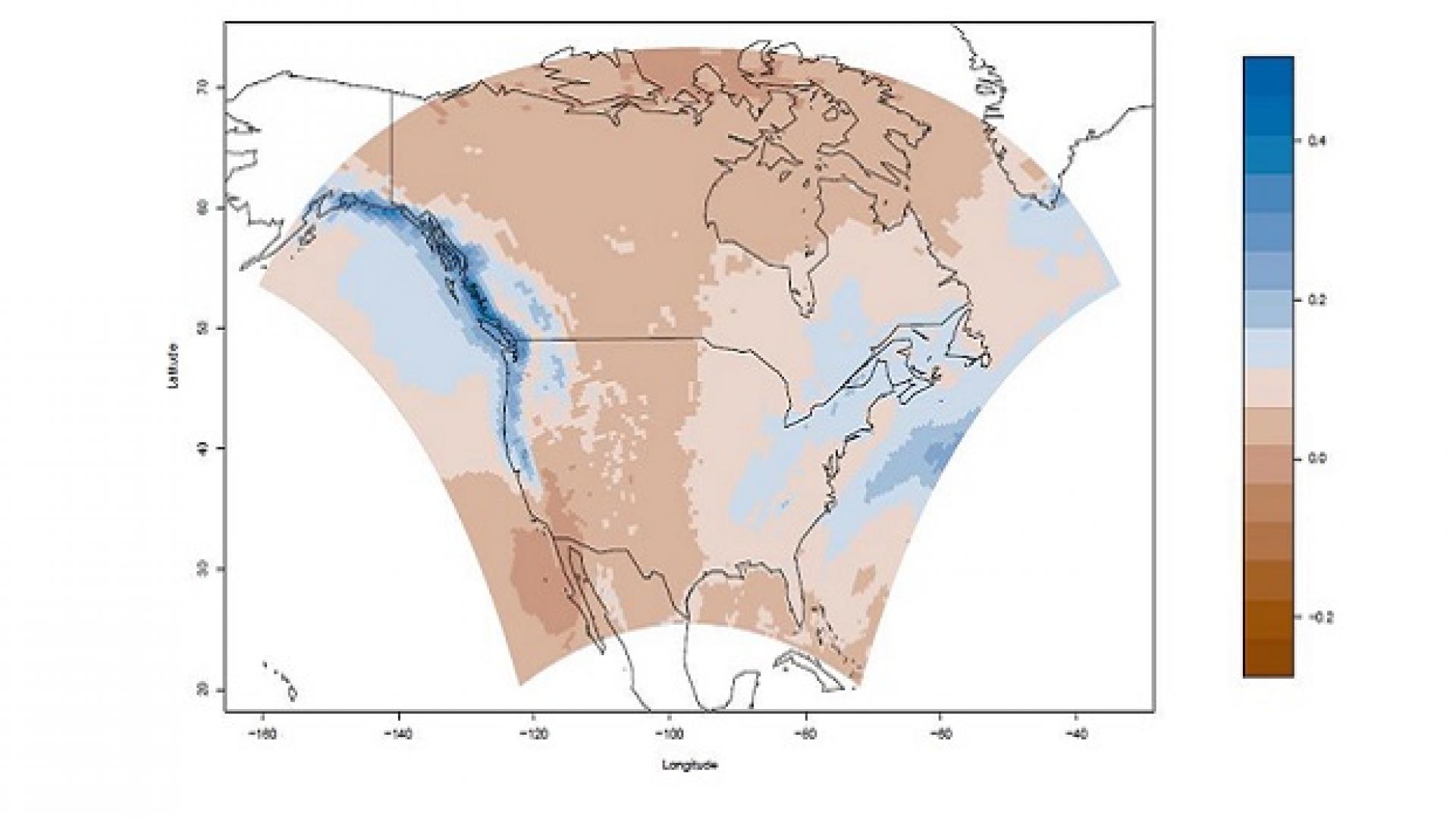
“Statisticians attempt to avoid unrealistic assumptions in order to estimate environmental processes more accurately,” says Li, a Ph.D. student in Sun’s research team. “The motivation behind our study was to improve how spatial nonstationarity is accounted for in climate modeling over a large and geographically complex area.”
Nonstationarity occurs when the statistics of an observed parameter, such as temperature or rainfall, varies over time or space. In this case, Li and Sun looked at the statistics that describe how measurements at two different locations change spatially. Understanding and accurately characterizing this covariance is critical in predicting weather and in translating or downscaling global climate modeling that is done at very coarse scales to be able to predict local effects at finer scales.
“We can think of spatial covariance as how well observations are correlated with each other in space, or as spatial patterns,” explains Li. “For environmental data, the spatial correlation pattern over land is different from that over the ocean. Because the correlation pattern is not exactly the same everywhere, we need to consider how to represent this nonstationarity.”
Nonstationarity has been dealt with previously by complex and computationally intensive convolution-based approaches, coupled with approximations based on assumptions of local stationarity at an arbitrary grid size. Sun and Li developed a computationally efficient approach that greatly improves the accuracy of approximation.
“The challenge for nonstationary modeling is the trade-off between accuracy and efficiency,” says Li. “We extended the local stationary model, which is efficient but not accurate, to a linearly varying local nonstationary model by dividing up the spatial region and estimating the covariance functions for each subregion. This allows us to describe more complicated nonstationary features, which improves accuracy while still being fast to compute.”
Read the full article