© ProStockStudio/ Shutterstock.com
A framework that uses graph theory, which considers how networks are coded, could help make digital communication networks more efficient.
For modeling social networks, no branch of mathematics is more integral than graph theory. The standard representation of a social network, in fact, is a graph. It comprises a set of points with lines joining some of the points. The points represent the network’s members, while the lines represent the connections between them.
Working with KAUST’s Tareq Al-Naffouri and Mohamed-Slim Alouini, former KAUST student Ahmed Douik now at Caltech and former postdoc Hayssam Dahrouj now at Effat University, have found a further area to which graph theory can be usefully applied: communications and signal processing.
“We’ve built a framework for using graph theory to solve problems of discrete optimization with excellent results,” says Dahrouj. Their method is to formulate a given digital communication network as a graph and then find “cliques” within it. In graph theory, this is known as solving the "clique problem."
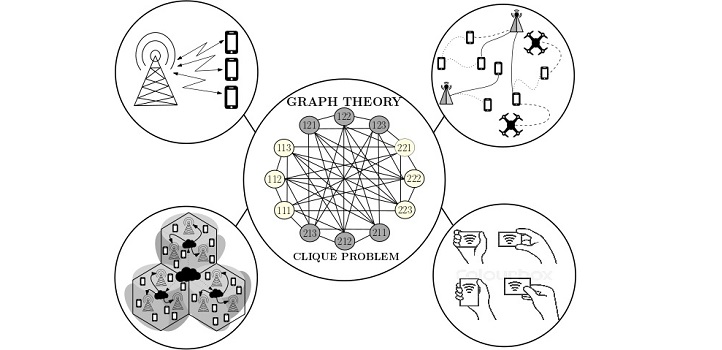
In any graph, a clique is a subset of points in which each point is connected to every other point. In a social network that means a group in which each member is friends with every other member in the group. Facebook, for example, solves the clique problem to work out the optimum friend suggestions and advertisements to send each of its many millions of members.
Read the full article


