We are proud to announce a significant achievement by our research team: the acceptance of our paper, "Approximating Hessian matrices using Bayesian inference: a new approach for quasi-Newton methods in stochastic optimization," in the prestigious journal Optimization Methods and Software. This work is a collaborative effort by André Carlon, a postdoctoral fellow at the Stochastic Numerics group at KAUST, Raúl Tempone, the PI of the group, and Luis Espath, a professor at the University of Nottingham.
Our research presents a novel approach to improving the performance of stochastic optimization methods, which are crucial for solving complex problems in various fields such as machine learning, finance, and engineering. By introducing a Bayesian framework for approximating Hessian matrices, we provide a new tool for enhancing the convergence and stability of optimization algorithms.
For those interested in learning more about this work, the preprint is available here, and a video presentation by André Carlon at the Stochastic Numerics and Statistical Learning Workshop 2023 is available here.
We are excited about the potential impact of our findings and look forward to further exploring and expanding upon this research. Stay tuned for more updates from our team!
Abstract
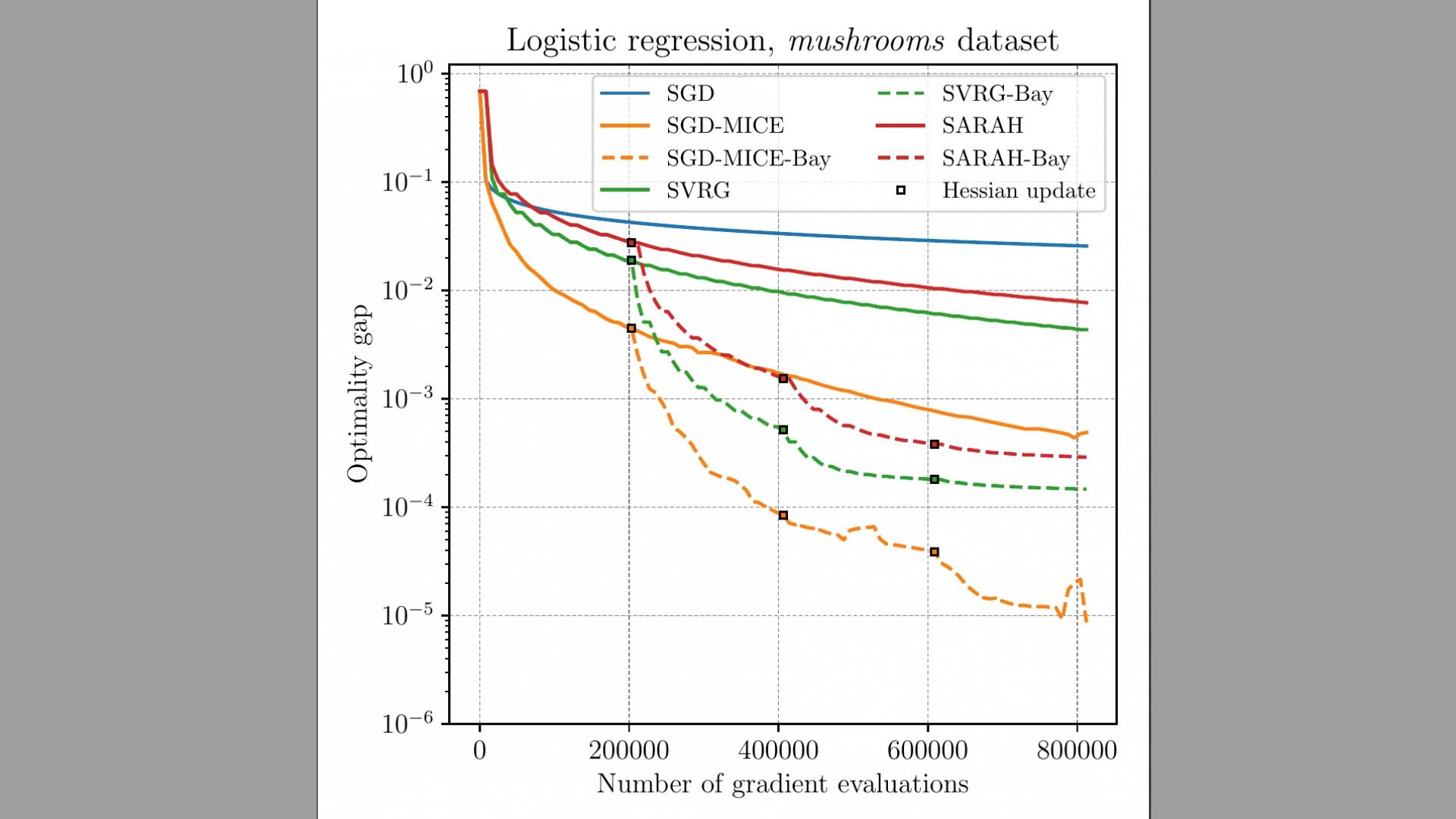
Using quasi-Newton methods in stochastic optimization is not a trivial task given the difficulty of extracting curvature information from the noisy gradients. Moreover, pre-conditioning noisy gradient observations tend to amplify the noise. We propose a Bayesian approach to obtain a Hessian matrix approximation for stochastic optimization that minimizes the secant equations residue while retaining the extreme eigenvalues between a specified range. Thus, the proposed approach assists stochastic gradient descent to converge to local minima without augmenting gradient noise. We propose maximizing the log posterior using the Newton-CG method. Numerical results on a stochastic quadratic function and an $\ell_2$-regularized logistic regression problem are presented. In all the cases tested, our approach improves the convergence of stochastic gradient descent, compensating for the overhead of solving the log posterior maximization. In particular, pre-conditioning the stochastic gradient with the inverse of our Hessian approximation becomes more advantageous the larger the condition number of the problem is.