We aim to use a multiscale sequential Bayesian inference approach. It is multiscale because we have a continuous-time discrete-state pure jump process base microscopic model and then two levels of approximation. First, a chemical Langevin diffusion, which is a continuous-time, continuous state stochastic approximation of the base model. Finally, by neglecting the brownian noise we arrive at a deterministic mean-field approximation.

Cylinder liners of diesel engines used for marine propulsion are naturally subjected to a wear process and may fail when their wear exceeds a specified limit. Since failures often represent high economical costs, it is utterly important to predict and avoid them.

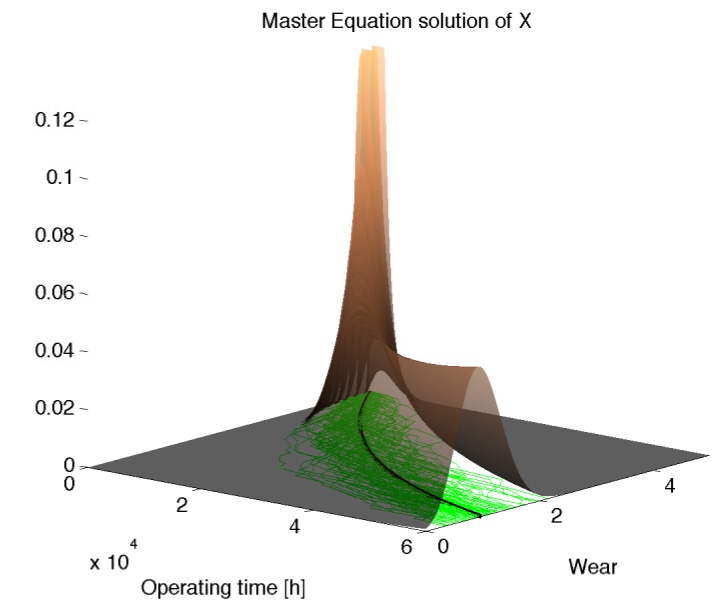
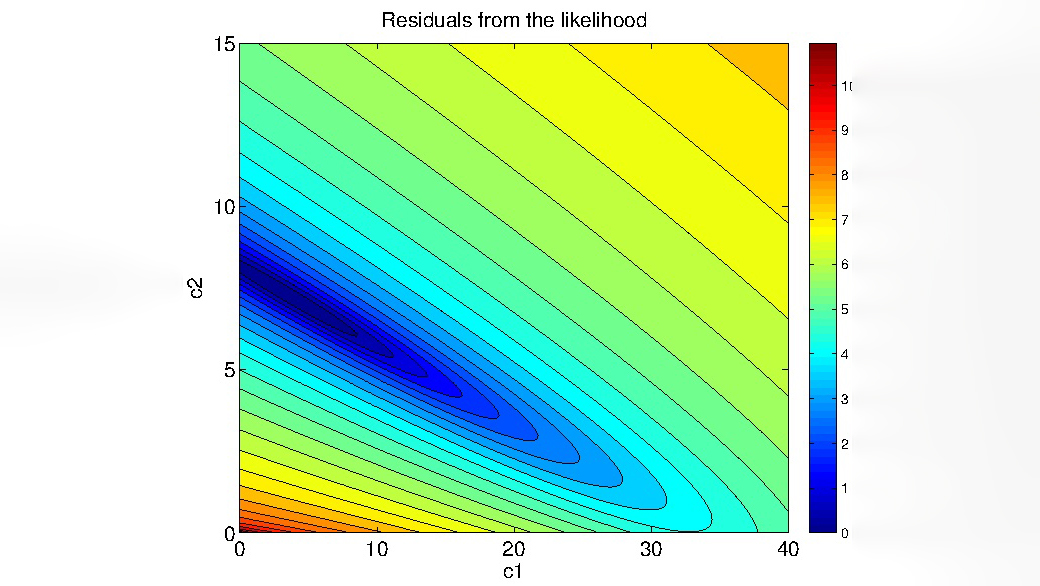
In this application, we model the wear process using a pure jump process, and therefore the inference goal is to estimate the coefficients and amplitudes of the jump intensities. We found that using a Gaussian approximation based on moment expansions it is possible to accurately estimate the jump intensities and amplitudes. We obtained results equivalent to the state of the art but using a simpler and less expensive approach.

Collaborators

Alvaro Moraes (KAUST)
Fabrizio Ruggeri (Politecnico di Milano)
Raul Tempone (KAUST)
Pedro Vilanova (KAUST)​

Publications

• A. Moraes, F. Ruggeri, R. Tempone and P. Vilanova. Multiscale Modeling of Wear Degradation in Cylinder Liners.​ Multiscale Modeling & Simulation, 12(1):396-409, 2014.