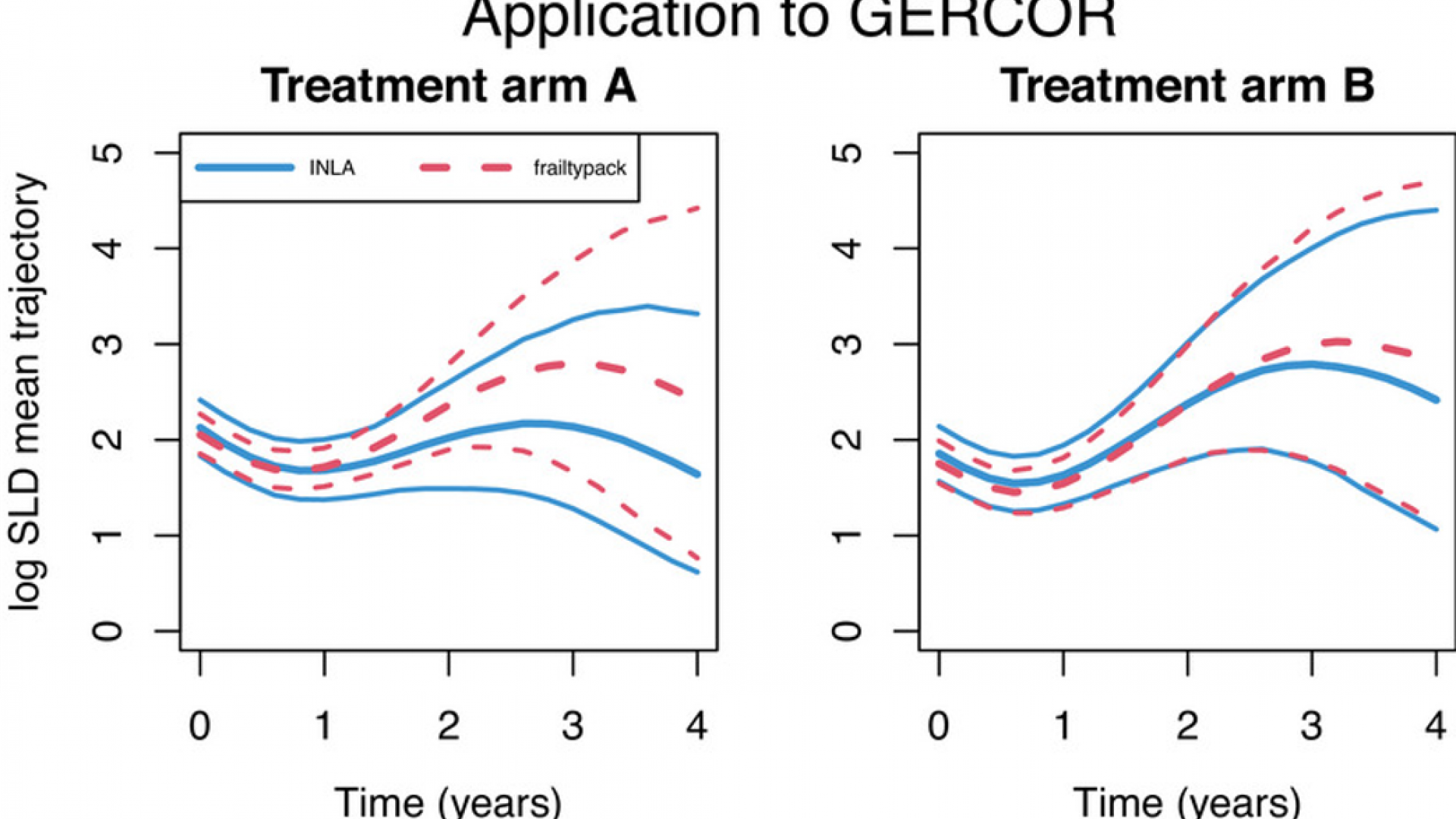
Two-part joint models for a longitudinal semicontinuous biomarker and a terminal event have been recently introduced based on frequentist estimation. The biomarker distribution is decomposed into a probability of positive value and the expected value among positive values. Shared random effects can represent the association structure between the biomarker and the terminal event. The computational burden increases compared to standard joint models with a single regression model for the biomarker. In this context, the frequentist estimation implemented in the R package frailtypack can be challenging for complex models (i.e., a large number of parameters and dimension of the random effects). As an alternative, we propose a Bayesian estimation of two-part joint models based on the Integrated Nested Laplace Approximation (INLA) algorithm to alleviate the computational burden and fit more complex models. Our simulation studies confirm that INLA provides accurate approximation of posterior estimates and to reduced computation time and variability of estimates compared to frailtypack in the situations considered. We contrast the Bayesian and frequentist approaches in the analysis of two randomized cancer clinical trials (GERCOR and PRIME studies), where INLA has a reduced variability for the association between the biomarker and the risk of event. Moreover, the Bayesian approach was able to characterize subgroups of patients associated with different responses to treatment in the PRIME study. Our study suggests that the Bayesian approach using the INLA algorithm enables to fit complex joint models that might be of interest in a wide range of clinical applications.