‌Time Domain Integral Equation (TDIE)-Based Solvers

The popularity of marching-on-in-time based TDIE (MOT-TDIE) solvers has increased following the development of acceleration engines such as plane wave time domain and time domain adaptive integral methods (TDAIM), as well as techniques for stabilizing TDIE solutions. Nowadays, accelerated and stabilized MOT-TDIE solvers favorably compete with finite difference solvers in the analysis of many real-world problems.

Even though MOT-TDIE solvers represent a rapidly maturing technology, there remain great opportunities for radical improvement. We are currently working on extending MOT-TDIE solvers, which have been originally developed for analyzing wave interactions in microwave frequency band, to allow for characterization of optical and photonic devices. During this process we are specifically working on new stabilization techniques, hybridization with time domain finite element methods, the formulation of new TDIEs suitable for modeling wave interactions in nonlinear and dispersive materials, and the use of non-uniform FTTs (NUFFTs) for accelerating the MOT process.

Hybrid Time Domain Simulators for EMI/EMC Analysis

The computational characterization of EMI/EMC phenomena on fully-loaded electrically large platforms (such as modern airborne and ground vehicles replete with cable-interconnected electronic systems) faces two important challenges. First, the simulator must be computationally efficient and offer multiscale modeling capabilities to permit the analysis of electromagnetic phenomena on electrically large platforms loaded with (sub)wavelength-scale systems. Second it must be able to account for uncertainty in the system configuration (viz. placement of the electronic systems and cables, parameterization of device and circuit descriptions, etc.), and the electromagnetic excitation.

A recently developed hybrid TDIE-based deterministic solver has (mostly) addressed the first challange. The second challenge still needs to be addressed. While, on the surface, Monte Carlo methods appear to be a good choice to account for the uncertainty in the system configuration, they require far too many deterministic function evaluations (i.e. costly EMI/EMC simulations) to be practical. A promising approach our group working on (in colloboration with University of Michigan) involves the use of (adaptive) polynomial chaos based stochastic collocation methods, which require far fewer function evaluations. 

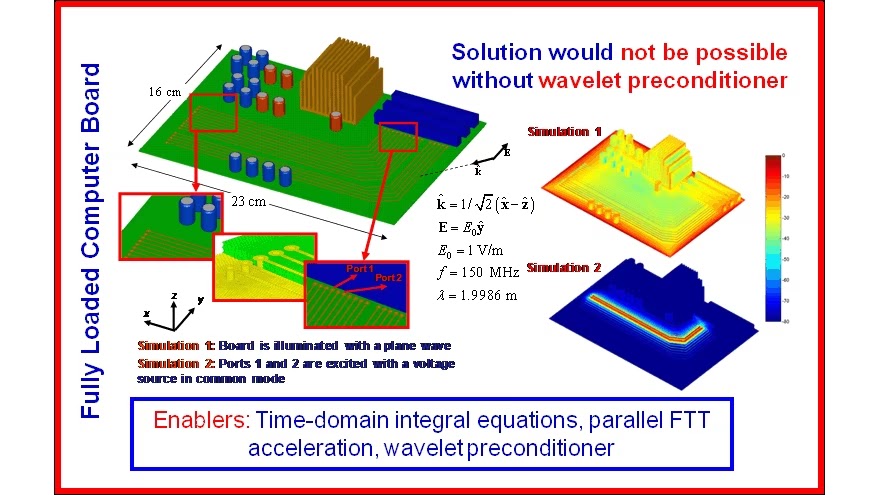
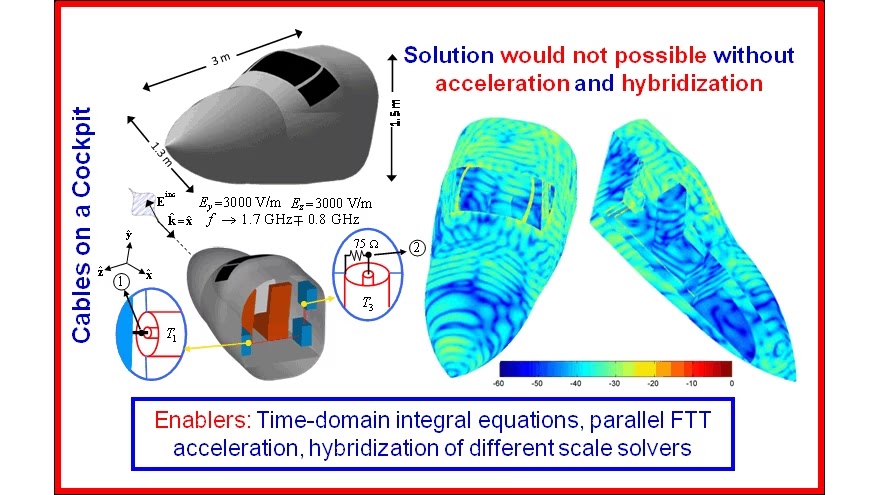
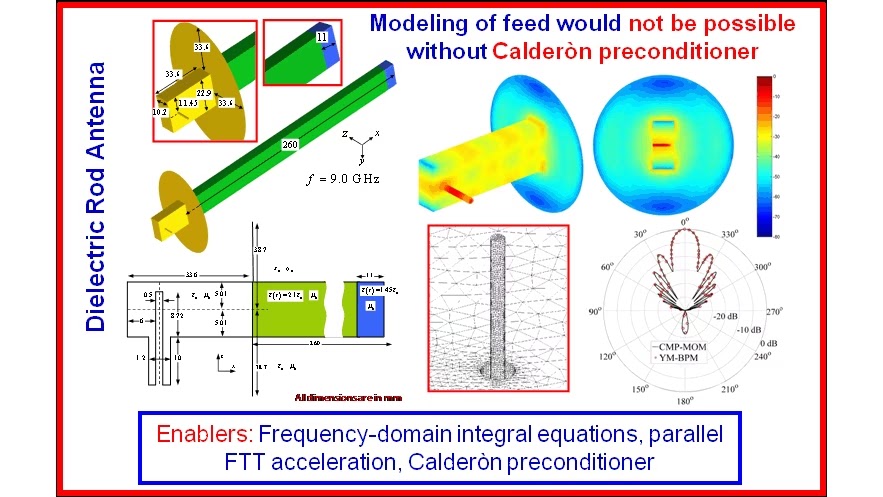
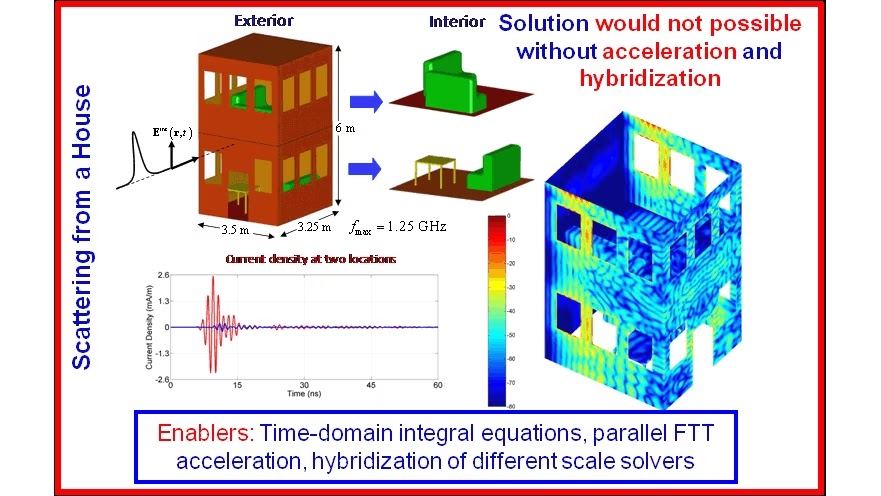
Time Domain Discontinous Galerkin Finite Element (TD-DG-FEM)-Based Solvers

TD-DG-FEM can be considered as a hybrid between finite element and finite volume methods, has several different variations. However, all these variations share three main characteristics that allow them to be explicit and (spatially) high order accurate: (i) the solution is piece-wise smooth, often represented by high order polynomials, but discontinuous between elements; (ii) boundary conditions and interface continuity are enforced only weakly; and (iii) all operators are local.

To achieve high order accuracy (in space and time), TD-DG-FEM has to employ a high order ordinary differential equation (ODE) solver for time-stepping to match the high order accurate spatial expansion of the solution. Currently our group is working on developing a new highly accurate and efficient marching-on-in-time scheme to used inconjunction with TD-DG-FEM. The resulting TD-DG-FEM - based solver will be used for characterization of high-frequency wave interactions with optical and photonic devices.

Finite Difference Time Domain (FDTD)-Based Solvers

FDTD-based methods are among the most widespread techniques in the field of CEM computational electromagnetics because they are straightforward to implement and parallelize, fully explicit, and can easily be extended for analysis of wave interactions in inhomogeneous media. However, when they are applied to the analysis of wave interactions in open regions, the computation domain should be artificially truncated. The most well-known solutions to this problem are based on Absorbing Boundary Conditions (ABCs) and Perfectly Matched Layers (PMLs). However none of these methods provides analytical tools for estimating a priori the error introduced in the final result, which comes with approximate computation-domain truncation. Furthermore, the level of error introduced increases drastically with the increasing length of the observation time, which is typically needed during analysis of resonance problems.

Currently we are working on developing FFT-accelerated non-local exact boundary conditions for accurately terminating open computational domains during FDTD-based simulations. Future research avenues under this project involves hybridization of FDTD with TDIE for even more accurate represenation of absorbing boundaries.

Localized Waves

Spatially and temporally localized electromagnetic pulses that propagate long distances without exhibiting diffraction and dispersion has been a subject of interest in the past few years due to their applications in high-speed and long-distance communication, energy transfer, and medical radiography.

Under this project, we study numerically the propagation of finite energy localized pulses in dispersive media. The numerical investigation is performed using time domain finite element and finite difference time domain methods, which are specifically designed for characterizing wave interactions in dispersive media. Future research topics include characterization of localized wave propagation in inhomogeneous (and dispersive) media.