A preprint of a new research project of our group named "Approximating Hessian matrices using Bayesian inference: a new approach for quasi-Newton methods in stochastic optimization" is available at arXiv. The manuscript is authored by André Carlon, Prof. Luis Espath, and Prof. Raúl Tempone.
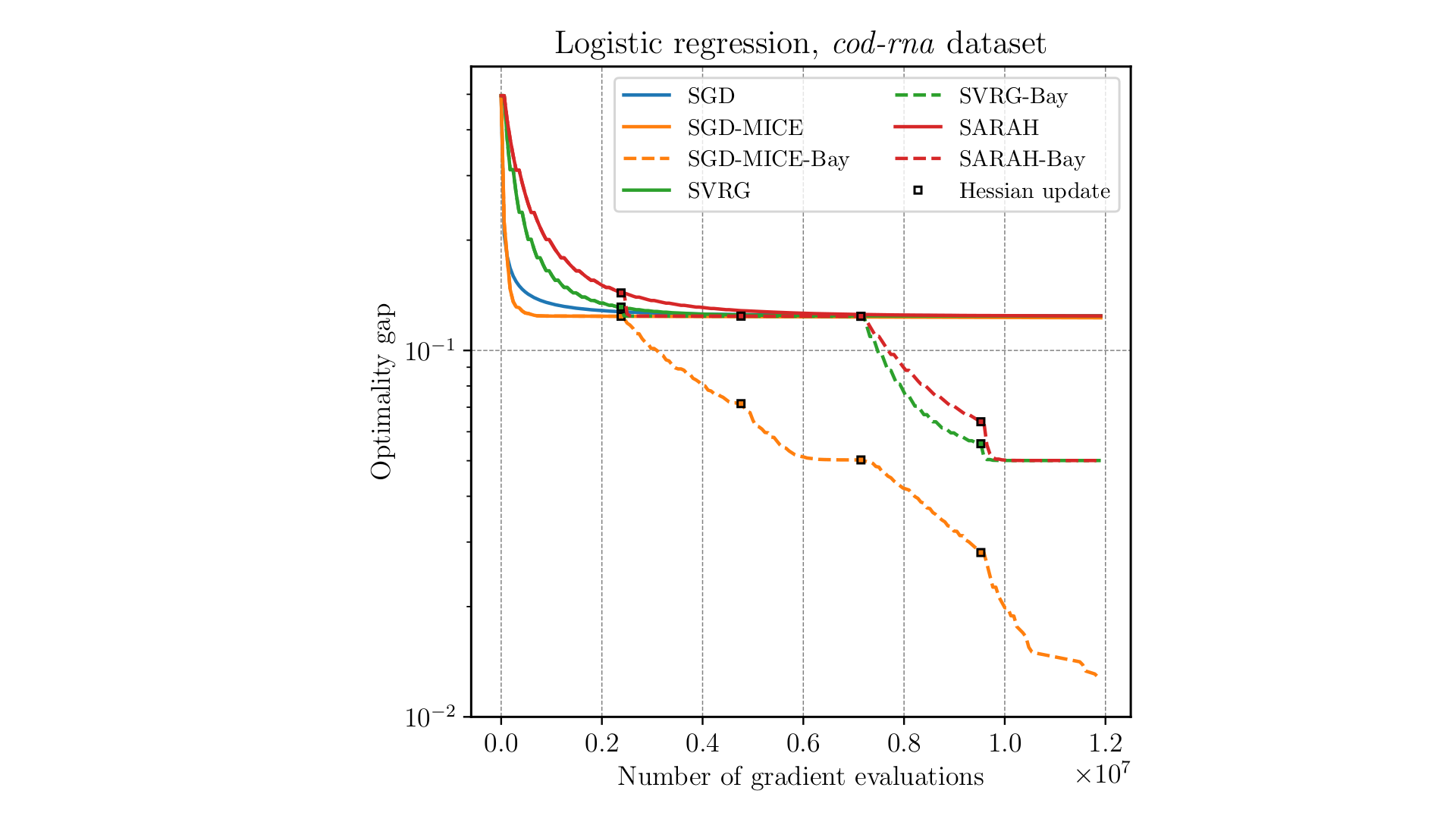
Abstract: Using quasi-Newton methods in stochastic optimization is not a trivial task. In deterministic optimization, these methods are often a common choice due to their excellent performance regardless of the problem's condition number. However, standard quasi-Newton methods fail to extract curvature information from noisy gradients in stochastic optimization. Moreover, pre-conditioning noisy gradient observations tend to amplify the noise by a factor given by the largest eigenvalue of the pre-conditioning matrix. We propose a Bayesian approach to obtain a Hessian matrix approximation for stochastic optimization that minimizes the secant equations residue while retaining the smallest eigenvalue above a specified limit. Thus, the proposed approach assists stochastic gradient descent to converge to local minima without augmenting gradient noise. The prior distribution is modeled as the exponential of the negative squared distance to the previous Hessian approximation, in the Frobenius sense, with logarithmic barriers imposing extreme eigenvalues constraints. The likelihood distribution is derived from the secant equations, i.e., the probability of obtaining the observed gradient evaluations for a given candidate Hessian approximation. We propose maximizing the log-posterior using the Newton-CG method. Numerical results on a stochastic quadratic function and a ℓ2-regularized logistic regression problem are presented. In all the cases tested, our approach improves the convergence of stochastic gradient descent, compensating for the overhead of solving the log-posterior maximization. In particular, pre-conditioning the stochastic gradient with the inverse of our Hessian approximation becomes more advantageous the larger the condition number of the problem is.