Khaled Moaddy, et al., "The fractional-order modeling and synchronization of electrically coupled neuron systems" Computers and Mathematics with Applications 64 (10), 2012, 3329.
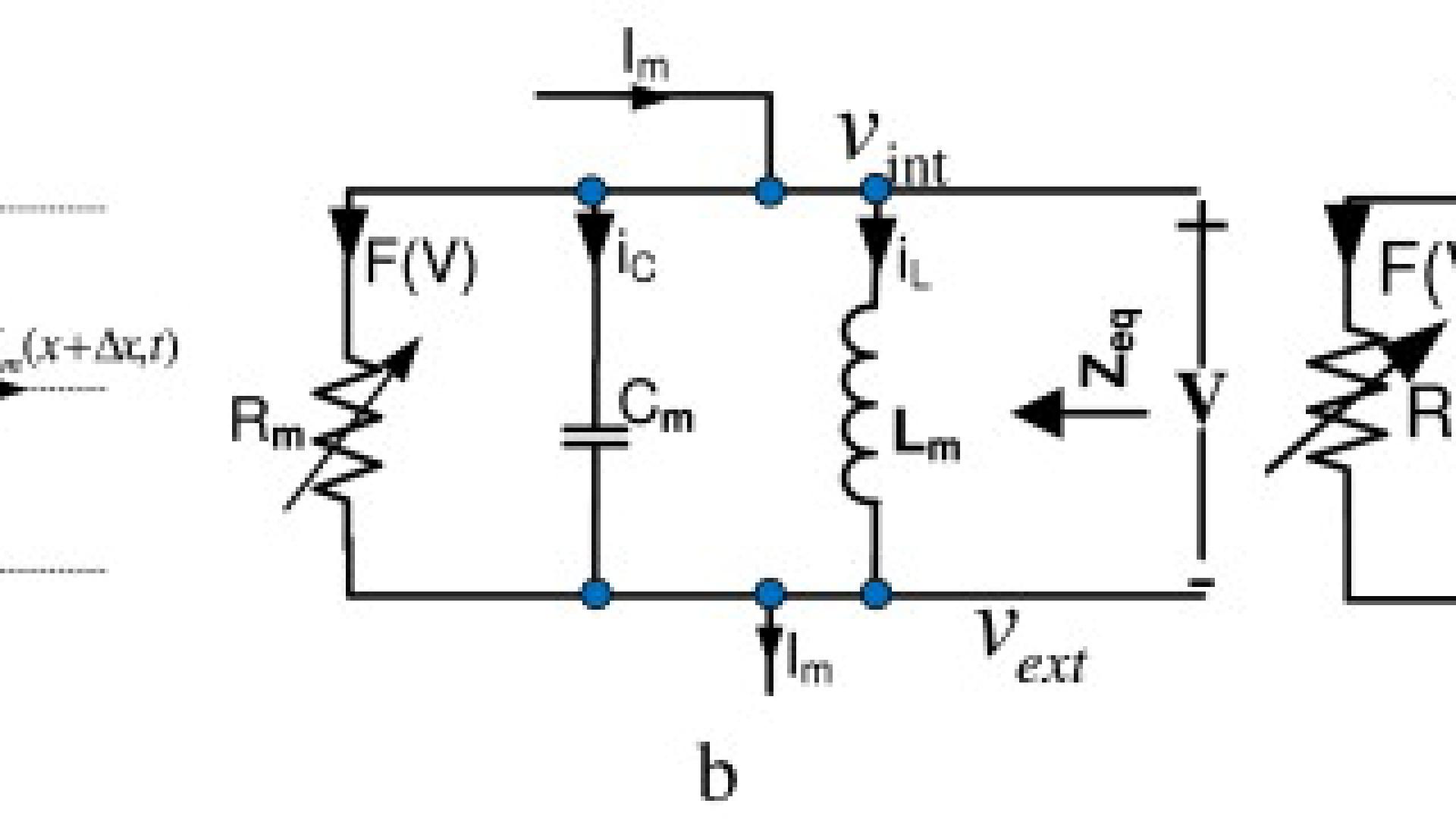
Abstract: In this paper, we generalize the integer-order cable model of the neuron system into the fractional-order domain, where the long memory dependence of the fractional derivative can be a better fit for the neuron response. Furthermore, the chaotic synchronization with a gap junction of two or multi-coupled-neurons of fractional-order are discussed. The circuit model, fractional-order state equations and the numerical technique are introduced in this paper for individual and multiple coupled neuron systems with different fractional-orders. Various examples are introduced with different fractional orders using the non-standard finite difference scheme together with the Grünwald–Letnikov discretization process which is easily implemented and reliably accurate.