2019 Maxat Kulmanov
A mathematical framework that bridges the gap between high-level human-readable knowledge and statistical data has been developed by a KAUST team and is expected to improve machine learning.
Humans rely on patterns, labels and order to make sense of the world. We categorize, classify and make links between related things and ideas, creating symbols that we can use to share information. Artificial intelligence, on the other hand, is trained most effectively using raw numerical data. How, then, can artificial intelligence algorithms make use of our vast store of symbolic knowledge? This is a vexing problem and one that, if cracked, could open an enormous new multidimensional library for machine learning and artificial intelligence.
Robert Hoehndorf, Maxat Kulmanov and their collaborators at KAUST’s Computational Bioscience Research Center and Halifax University, Canada, have developed a mathematical bridge between these seemingly incompatible forms of information.
“There is a big gap in artificial intelligence research between approaches based on high-level symbolic representations understandable by humans and the subsymbolic approaches used for training artificial neural networks,” explains Kulmanov. “Symbolic approaches are built on logical relationships, while subsymbolic approaches rely on statistics and continuous real-numbered vector spaces.”
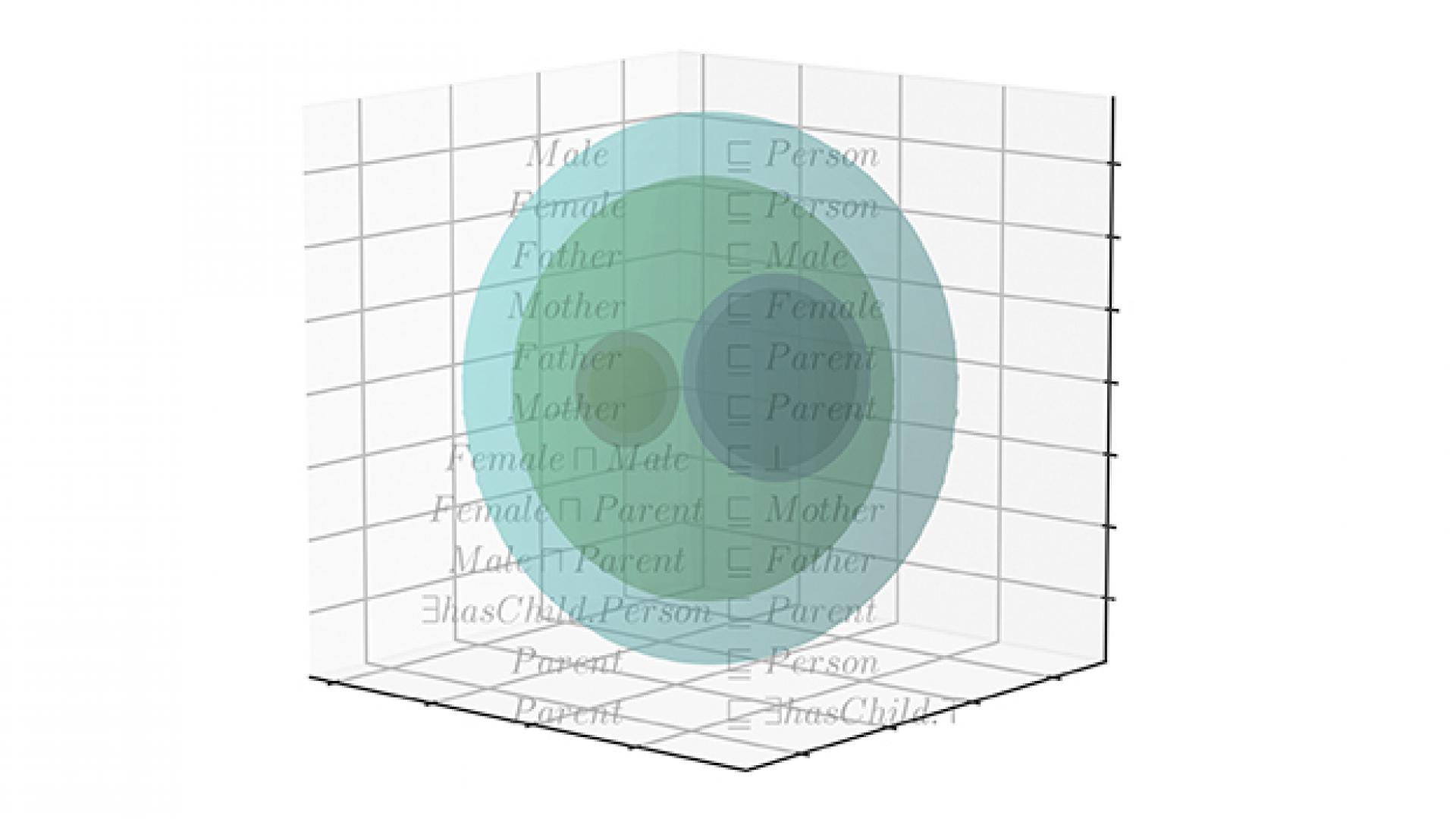
The researchers set out to develop an "embedding" function that maps one mathematical structure to another in a way that preserves some of the features of the first structure.
“Embeddings are used because the second structure may be more suitable for some operations,” says Hoehndorf. “In this work, we mapped a formal language, called a description logic, into a real-number vector space, which can be used more easily for machine learning, such as computing similarity and performing predictive operations.”
Description logics are widely used in biology and biomedicine to describe formalized theories, such as the functions of genes and the terminology used in medical diagnosis.
“Logics, such as description logic, have been the foundation for artificial intelligence systems since the 1960s and have been studied in mathematics for more than 100 years,” says Hoehndorf. “Building on this history of research, we created an embedding function that not only projects symbols into a vector space, but also generates algebraic models to capture the semantics of the symbols within description logic.”
Read the full article